Numerical Integration in Python
Recently, I've started looking into TensorFlow and what's being called "deep learning" (i.e. neural networks), and I've discovered as I try to read through the algorithms that my calculus has gotten a bit rusty. Of course, it's entirely possible to read through the descriptions of the algorithms involved without fully understanding the theory behind them, but I understood the background just well enough that I kept being irritated that I couldn't put the whole story together. I did take three semesters of undergraduate calculus, after all — I knew this stuff at one time. As it turns out, since I hadn't been able to sell my calculus textbook back to the campus bookstore because it was an old edition, I actually still have it. So I dug it out, dusted it off, and started reading over the chapters on partial differentiation and multiple integrals. I was pleasantly surprised how quickly and easily it came back to me. (Which bodes well, because I'm going to be helping my son with his calculus homework when he starts his junior year of high school in a few years).
Of course, being a math textbook, my calculus book is full of back-references to previous chapters. I came across one back reference that I remember despising as an undergraduate: Simpson's rule. See, if you can't find a closed- form integral for a particular function (or if you don't even actually have a continuous function to integrate), you can estimate the definite integral by evaluating the function at specific points. So, for example, to compute:
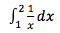
(to approximate the ln function, for example), you could evaluate:
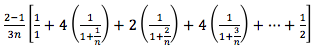
This can be geometrically interpreted as the shaded area in the graph shown in figure 1, below:
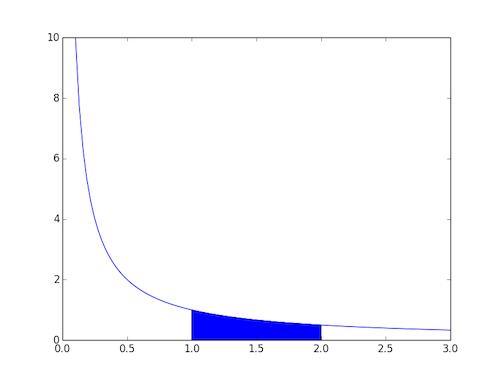
Figure 1: The ln function
More generally, the definite integral of any function can be estimated by:
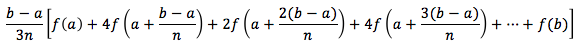
For some function f and some n — the larger the better. There's a whole theory of why this works based on approximations of parabolas in the spaces between each 1/n increment of the function evaluation that you can look up if you're curious.
As I look at some of the example homework problems, I'm reminded of exactly why I hated this topic so much: estimating definite integrals by way of Simpson's rule is tedious with a hand calculator, which is what we had to work with back in the 80's. (Well, actually we did have computers back then, too, but we weren't allowed to use them in exams). I remember hand-tabulating long tables of values like this one:
| k | xk | f(xk) | m | mf(xk) |
|---|---|---|---|---|
| 0 | 1.0 | 1.0 | 1 | 1.0 |
| 1 | 1.1 | 0.90909091 | 4 | 3.636363 |
| 2 | 1.2 | 0.83333333 | 2 | 1.666667 |
| 3 | 1.3 | 0.76923076 | 4 | 3.076923 |
| 4 | 1.4 | 0.71428571 | 2 | 1.428571 |
| 5 | 1.5 | 0.66666667 | 4 | 2.666667 |
| 6 | 1.6 | 0.625 | 2 | 1.25 |
| 7 | 1.7 | 0.58823529 | 4 | 2.352941 |
| 8 | 1.8 | 0.55555556 | 2 | 1.111111 |
| 9 | 1.9 | 0.52631578 | 4 | 2.105263 |
| 10 | 2.0 | 0.5 | 1 | 0.5 |
I was struck immediately by how naturally this fits the functional programming paradigm, so I put together a quick Python program to work some of the examples:
from __future__ import division
def simpson(a, b, n, f):
sum = 0
inc = (b - a) / n
for k in range(n + 1):
x = a + (k * inc)
summand = f(x)
if (k != 0) and (k != n):
summand *= (2 + (2 * (k % 2)))
sum += summand
return ((b - a) / (3 * n)) * sum
# Examples of use
print(simpson(1, 2, 10, lambda x: 1 / x))
print(simpson(1, 4, 6, lambda x: 1 / x))
import math
print(simpson(0, 1, 6, lambda x: 1 / math.sqrt(1 + x * x)))
Listing 1: Simpson's rule in Python
The simpson function keeps track of the running sum and the
multiplicands associated with each evaluation of the function, but the
function to be evaluated is, itself, an actual python function that takes in
a single argument x and returns its value.
A related rule called the trapezoidal rule yields similar results:
from __future__ import division
def trapezoid(a, b, n, f):
sum = 0
inc = (b - a ) / n
for k in range(n + 1):
x = a + (k * inc)
summand = f(x)
if (k != 0) and (k != n):
summand *= 2
sum += summand
return sum * ((b - a) / (2 * n))
# Example of use
print(trapezoid(1, 2, 10, lambda x: 1 / x))
Listing 2: Trapezoidal rule
As well as the "midpoint" rule that evaluates the function in between each point in the intervals:
from __future__ import division
def midpoint(a, b, n, f):
sum = 0
x_int = ((2 * n + 1) * a - b) / (2 * n)
inc = (b - a) / n
for k in range(1, n + 1):
x = x_int + (k * inc)
sum += f(x)
return sum * inc
# Example of use
print midpoint(1,2,10,lambda x: 1/x)
Listing 3: Midpoint rule in Python
Of course, all of this is already implemented in scipy, surely
much faster than this implementation, but I thought it was interesting to put
together.
Add a comment:
Completely off-topic or spam comments will be removed at the discretion of the moderator.
You may preserve formatting (e.g. a code sample) by indenting with four spaces preceding the formatted line(s)


The articles are incredible.
The way they all are directing to achieving the common goal of theDummy-fication of sec trusted things. x5.
Exactly 0.5 year ago i Got digging into asn binaries, working on understanding the raw bits positioning of results from OCSP response
that i was getting from my own made CA structures and certs.. nice time crossing.
..
Saying it in a form of retrospection... :
..
I was laying silently this night and i did not knew why i got so obsessed over Your article for OCSP response signing and then it hit me!!
AAAAAll the other articles, so strangely familiar to me personal exp and The Code Of Words (Yours) in some critically planned places; the meaning behind it and understanding of the simplicity from a almost HelloWorld perspective, showing --==ALL==-- BUT not Revealing it in obvious words! [ how to "break Things" vs "rearrange in MY way" someone's toys/bricks of Public Trust. Complexity that is brought to the World, is falling to the quants of information in the "muted suggestions".
The GIF dissection (usage in pimping-out the styling of greenBars... EHH :-) ; the GZIP dissection; signature breaking into simplicity and CRC3 loading -> all being a driver for the pining of ??Trust??. All this allowing to experiment to have complete control over what WAS sometime ago secure.
I am a self learner and I always got a need to have the asm-alike lvl of knowing how things work, and the Sec Layers of nowadays tech and it's objectives, seemed to be attracting me always. Somehow adding to my life surprising coincidences of software bugs (and later R&D-over-it), functionality dilemmas directing Me in a way Your ARTs do with so incredible alignment in covered topics.
Thank You For the knowledge You share.
I will keep me silent to the findings I make, but will for sure spread the knowledge but in a way You do.
[a unopened pre